 |
 |
This series was developed after one on exploring a container; a non-traditional container that cannot holds anything. This container is at one level representing a functional object and another a dis-functional object. Given this, the form and surface can be reformulated and deviate from traditional meanings. The overall form can also express containing a more interconnected volume, since it cannot hold anything. The surface can be articulated in a number of ways, from smooth to texture. This series also explores 3D printing techniques in common materials that can structurally be very delicate; pushing the technology to its limits of defining enclosures and still be structurally viable. Forms and their structural enclosures can be explored in a number of ways, in a number of scales. Extrusions, assemblages, or incorporating traditional structural systems; or ones according to mathematically defined elements. What forms emerge when a 2D curve is used as a 3D path for some section defined by a simple shape, such as a circle, an ellipse, a square, a rectangle, or a triangle? This series investigates a simple form based on approximately one-half of a Lemniscate of Bernoulli curve, developed about 1694. It is very similar to a common eight curve, except the loops are more elliptical. For the enclosure a simple solid surface was incorporated. Custom software has been developed to generate these containers These containers are computationally generated, custom developed software; a method which can express a consistency of a developing a concept and enable a variety that focuses on the idea and its variations. Then the digital model is 3D printed in sandstone. |
 |
 |
Sandstone: 00_01e1a and 00_01d1a |
Sandstone: 01_01a1b and 01_01f1d |
 |
Sandstone: 08a347a5 and 08a347a7 |
 |
 |
 |
 |
00_01d1a_p1 |
00_01d1a_p1t |
00_01d1a_x2 |
00_01e |
 |
 |
 |
 |
00_01e1a_p1a_x |
00_01e1a_p1t |
00_01e1a_x2 |
00_02a1 |
 |
 |
 |
 |
00_02a2 |
00_02a3 |
00_02a4 |
00_02a5 |
 |
 |
 |
 |
00_03a1 |
00_03a3 |
00_03a5_x2 |
00_03b1 |
 |
 |
 |
 |
00_03b1_x2 |
00_03b2 |
00_03b2_x2 |
00_03b3 |
 |
 |
 |
 |
00_03b3_x2 |
00_03b4 |
00_03b4_x2 |
00_03b5_x2 |
 |
 |
 |
 |
00_03b6_x2 |
00_03b7_x2 |
00_03b8_x2 |
00_03b9_x2 |
 |
 |
 |
 |
00_03c1 |
00_03c2 |
00_03c3 |
00_03c4 |
 |
 |
 |
 |
00_03c5 |
00_04a1 |
00_04a3 |
00_04a5 |
 |
 |
 |
 |
00_04a5_x2 |
00_06a1_5a1 |
00_06a1_5a5 |
00_06a2_5a5 |
 |
 |
 |
 |
00_06a5_5a5 |
00_07a1 |
00_07a2 |
00_07a21 |
 |
 |
 |
 |
00_07a21c |
00_07a3 |
00_07a34 |
00_07a4 |
 |
 |
 |
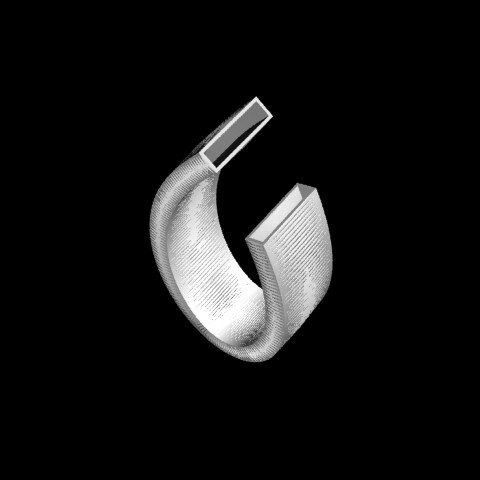 |
00_07a43 |
00_07a43c |
00_07a5 |
00_07a6 |
 |
 |
 |
 |
00_07a65 |
00_07a65c |
00_07a7 |
00_07a78 |
 |
 |
 |
 |
00_07a78c |
00_07a8 |
00_07a87 |
00_07a87c |
 |
 |
 |
 |
00_08a1 |
00_08a1234 |
00_08a127a6 |
00_08a2 |
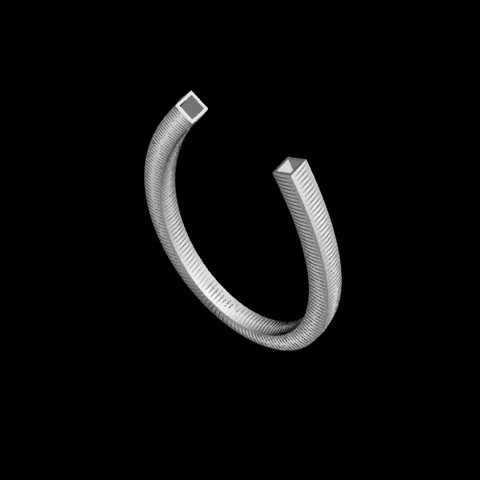 |
 |
 |
 |
00_08a3 |
00_08a347a5 |
00_08a4 |
00_08b12_1 |
 |
 |
 |
 |
00_08b34_2 |
00_09a1 |
00_10a1 |
00_10a2 |
 |
 |
 |
 |
00_10a3 |
00_10a4 |
00_10a5 |
00_10a6 |
 |
 |
 |
 |
01_01a |
01_01a0_p3 |
01_01a0_s |
01_01a0_sh |
 |
 |
 |
 |
01_01a0_x |
01_01a0_x2 |
01_01a0_x2_s |
01_01a0_x2r |
 |
 |
 |
 |
01_01a0_x2x |
01_01a0a_p4 |
01_01a0a_x2_p4 |
01_01a0a_x2r |
 |
 |
 |
 |
01_01a0a_x2x_p4 |
01_01a0g |
01_01a0g_x2 |
01_01a0h |
 |
 |
 |
 |
01_01a0h_x2 |
01_01a0i |
01_01a0i_x2 |
01_01a0j |
 |
 |
 |
 |
01_01a0ji_x2 |
01_01a1a |
01_01a1b_p2 |
01_01a1b_p2t |
 |
 |
 |
 |
01_01a1b_x |
01_01a1b_x2 |
01_01a1b_x2a |
01_01a1b_x2b |
 |
 |
 |
 |
01_01a1b_x2r |
01_01f1a |
01_01f1b |
01_01f1b_x2 |
 |
 |
 |
 |
01_01f1b_x2r |
01_01f1c |
01_01f1c_x2 |
01_01f1c_x2r |
 |
 |
 |
 |
01_01f1d_p2 |
01_01f1d_p2t |
01_01f1d_x2 |
01_01f1d_x2r |